Time Value of Money Formula, Reasons, Factors and Techniques

Table of Contents:

• What is Time Value of Money?
• Time Value of Money Formula
• Reasons for Time Value of Money
• Factors Influencing Time Value of Money
• What is an interest?
  • Simple Interest
  • Compound Interest
• Future value
• Techniques of Time Value of Money

What is Time Value of Money?

The time value of money concept is a basic principle of finance. It refers to the fact that the money received today is different in its worth from the money receivable at some other time in future. In other words, the same principle can be stated that the money receivable in future is less valuable than the money received today. The concept of the time value of money is also referred to as the present discounted value.

As per the principle of the time value of money, money can grow only through investing so a delayed investment is a lost opportunity.

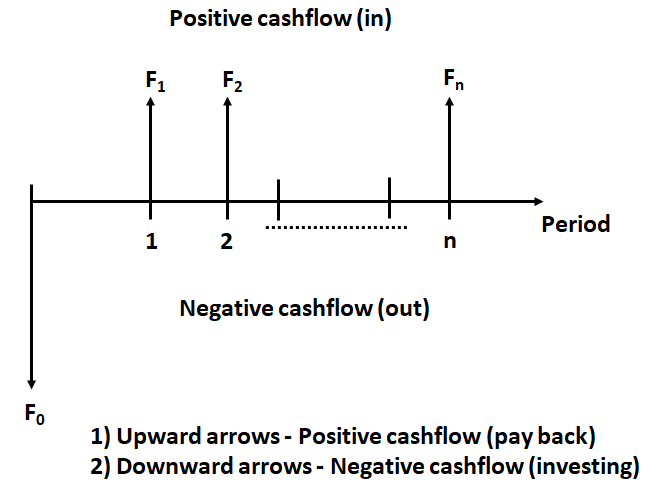
Unless otherwise indicated, all such cash flows are considered to occur at the end of their respective periods Cashflows can be positive and negative as shown in below figure:

For example, a company is selling a motor for ₹16,000. The buyer offers to pay 16,000 either now or after one year. The seller company will naturally accept the first offer, i.e., to receive ₹16,000 now. In this case, if the company reinvests the amount of ₹16,000 in the fixed deposit account for one year at 10% p.a. interest, then after one year the firm will have total money of 18,500 (₹16,000 + ₹2,500 interest). In the second option, the company will receive only ₹16,000 after one year. Therefore, in the first option, the company will be better off by ₹2,500.

On the other hand, if the buyer of the machine is ready to pay ₹.18,500 instead of ₹16,000 after one year, then the firm may be indifferent. In this situation, the firm will have 18,500 after one year either:

1) By receiving ₹16,000 now and reinvesting to get interest of 2,500, or

2) To get 18,500 from the buyer after one year. This interest amount of 2,500 is the time value of money.

Thus, the time value of money for the money is its rate of return which the firm can earn by reinvesting its present money. This rate of return can also be expressed as a required rate of return to equal the worth of money of two different periods. In simpler terms, the value of a certain amount of money today is greater than its value in the future. The difference between the value of money today and tomorrow is known as the time value of money.

Time Value of Money Formula

The fundamental formula for calculating the time value of money considers several key factors: the future value of money, the present value of money, the number of compounding periods per year, the interest rate, and the duration of years.

Based on these variables, the formula for the time value of money can be stated as:

$$\;\mathrm{FV}=\mathrm{PV}\left(1+\frac{\mathrm i}{\mathrm n}\right)^{\mathrm n\times\mathrm t}$$

Where:

• FV = Future value of money
• PV= Present value of money
• i = Interest rate
• n = Number of compounding periods per year
• t = Number of years​

Note: The Time Value of Money (TVM) formula may vary slightly depending on the specific situation. For example, in the case of perpetuity payments or annuities, the formula may include fewer or additional factors.

Reasons for Time Value of Money

Money has time value because of the following reasons:

1) Risk and Uncertainty

The future is always uncertain and risky. Cash outflow is in our control as payments to parties are made by us. The future cash inflows are uncertain. Cash inflow is dependent on our creditor, bank, etc. As individuals and businesses are not certain about future cash receipts, they prefer to receive cash immediately rather than waiting for future cash receipts.  

2) Preference for Consumption

Most people have a subjective preference for present consumption over future consumption of goods and services either because of the urgency of their present wants because of the risk of not being in a position to enjoy future consumption that may be caused by illness or death, or because of inflation. As money is how individuals acquire most goods and services, they may prefer to have money now.

3) Investment Opportunities

An investor can profitably employ a rupee received today, to give him a higher value to be received tomorrow or after a certain time.

4) Inflationary Economy

In an inflationary economy, the money received today has more purchasing power than the money to be received in future. In other words, the value of a rupee today holds greater real purchasing power than a rupee a year.

Factors Influencing Time Value of Money

The concept of the time value of money can be attributed to three fundamental reasons. These reasons are as follows:

1. Delay in opportunity cost
2. Inflation
3. Risk

All these factors have an impact on the value of money individually as well as in the combined form. Let us understand these factors:

1) Delay in Opportunity Cost

Opportunity cost delay results from the time value of money, highlighting the importance of obtaining funds in the present while also considering the trade-offs in choosing one option over another. This delay occurs when the opportunity cost of choosing one option over another is postponed due to the time value of money.

2) Inflation

The term Inflation is generally used to describe the increase in prices of goods and services. But what does it exactly mean? In simple terms, inflation refers to the decrease in the purchasing power of money.

For example, if you had ₹500 to purchase petrol a decade ago, you would have been able to buy a larger quantity compared to what you could buy with the same amount today. This represents how inflation reduces the value of money over time. It is important to understand that inflation greatly affects the time value of money.

3) Risk

Risk is a basic aspect of uncertainty. When considering the acquisition of future funds, we must acknowledge that we are essentially giving up a current opportunity and promoting associated risks. Put simply, opting not to receive money in the present equates to lending that money. This decision introduces default risk, including the possibility of not receiving any money back or, even worse, not receiving the entire amount back. Therefore, risk plays a major role in the concept of the time value of money.

What is an interest?

 It is the additional amount that accumulates on the principal amount borrowed or lent for a specific time. The time may vary depending on the specific requirements. The time may range from one week, one month to one year and so on. The time value of money is created due to the interest. Now, the question arises as to what is an interest rate.

Interest rates are generally expressed as percentage terms. They can be 1%, 2%, 10% and so on. It is the rate at which the interest accrues over time.

Interest is charged against the use of money paid by the borrower to the lender in addition to the actual money lent.

Types of Interest: There are two types of interests:

1. Simple Interest, 
2. Compound Interest.

Simple Interest

Simple interest is the interest that is calculated only on the original amount (principle), and thus, no compounding of interest takes place. Simple Interest is defined as the interest which is accrued only on the actual amount borrowed. The previous interest accrued but not paid/received is not included in the simple interest. The formula to calculate simple interest is:

SI = PV $\times$ r $\times$ t

Where:

SI = Simple Interest

PV= Money borrowed/lent at present

r = Interest Rate

t = Time Period

Let us understand it through an example.

 Que: Calculate the simple interest on a borrowed sum of money as Rs. 1,00,000 at 10% per annum in 3 years. Find the sum of money.

Ans: Computation of simple interest –

	Particulars	6 Months	1 Year	2 Year	3 Year
A	Money Borrowed	1,00,000	1,00,000	1,00,000	1,00,000
B	Interest rate annually	0.10	0.10	0.10	0.10
C	Time period in years	0.5	1	2	3
D	SI = PV$\times$ R$\times$ T	5,000	10,000	20,000	30,000

Compound Interest

Compound interest is the interest that is received on the original amount (principle) as well as on any interest earned but not withdrawn during earlier periods. Compounding is the process of finding the future value of cash flows by applying the concept of compound interest.

It is the interest which is accrued on the initial borrowed/lent amount along with the interest which is accrued previously but not paid/received.

In compound interest, each interest payment is reinvested to earn further interest in future periods. However, if no interest is earned on interest, the investment will only earn simple interest. In such a case, the investment grows as follows:

Future value $=PV+(1\; +r\times n)$

Where:

• PV = Present Value (initial investment or principal)
• r = Annual interest rate (expressed as a decimal)
• n = Number of years

For example: if 5,000 is invested @ 14% simple interest, in 5 years it will become 5,000 [1+5×0.14] = ₹8,500

To calculate Compound Interest, we use the following formula:

CI = FV – PV

CI = Compound Interest

FV = Future Value

PV = Present Value

A = P (1+r)

A = Amount at the end of a period

P = Principal Amount

r = Rate of Interest

t = Time period

An example is given below to make the concept more clear.

Que: Suppose Ms. Reena invests 20,000 at 5% interest to be compounded annually in a savings bank account. At the end of the year, Ms. Reena will have 21,000 in her account. This is the current principal amount which will earn interest in the upcoming year. This amount will become ₹22050/- at the end of the next year. This will then become the principal amount for the third year and so on. The table below shows the procedure of annual compounding:

Table: Annual Compounding

Year	1	2	3
Initial Amount (₹)	20,000	21,000	22,050
Rate of Interest	5%	5%	5%
Compound Interest	1000	1050	1102.5
Beginning Principle (₹)	20,000	20,000	20,000
Ending Principle (₹)	21,000	21,050	23152.5

This principle continues for some time till the account remains.

A = (1+ r)^t

1 year A = 20,000 (1+0.05)¹  = 21,000

2 year B = 20,000 (1+0.05)² = 22,050

3 year C = 20,000 (1+0.05)³ = 23152.5

CI = FV – PV

1 year = 21,000 – 20,000 = 1000

2 year = 22,050 – 21,000 = 1050

3 year = 23152.5 – 22,050 = 1102.5

Future value

Interest defines the future value of money. It is the money which is held at present for a given rate of interest in the future.

Therefore,

Future Value of Money = Present value + Simple Interest

FV = PV (1+r)^t

FV = Future Value

PV = Present Value

r = Rate of Interest

t = Time Period

Computation of Future Value at Simple Interest:

Que: What will be the future value of an amount of 2000 which is borrowed at interest of  5%?

	Particulars	6 Months	1 Year	2 Year	3 Year
A	Money Borrowed (₹)	2000	2000	2000	2000
B	Simple interest (SI = PV $\times$ r $\times$ t)	50	100	200	300
C	FV= PV + SI (₹)	2050	2100	2200	2300

Computation of Future Value at Compound Interest:

Que: What will be the future value and compound value of an amount of 20,000 which is borrowed at an interest of  10% annually for:

1. 1 year
2. 2 year
3. 3 year

Ans:  Formula :

• FV = PV (1+r)^t
• CI = FV – PV

Particulars	1 Year	2 Year	3 Year
Present value (amount borrowed ) (₹)	20,000	20,000	20,000
Rate of Interest	0.1	0.1	0.1
Time Period	1	2	3
Future value (₹)	22,000	24,200	26,620
Compound Interest (₹)	2000	4,200	6,620

Techniques of Time Value of Money

There are two techniques for adjusting the time value of money. They are:

Techniques of Time Value of Money

1. Concept of Present Value Discounting
2. Concept of Future Value Compounding

Present value refers to the current value of money that is either receivable or payable at a future date.  Similarly, the value of money at a future date with a given interest rate is called future value.

Reference:

• https://egyankosh.ac.in/bitstream/123456789/80034/3/Unit-2.pdf